Relative loss in integral field due to ends is considerable in superconducting magnets where the length of the straight section (or body) of the magnet becomes comparable to the two ends. The optimum integral design overcomes that loss by essentially extending the body or straight section of the magnet to the whole length of the coil. Picture below shows the body of the magnet extending almost the full length as compared to that in the other designs where ends (which are not efficient in creating field) take away significant space.
Coil of an Optimum integral design with body extending full length and essentially no loss from the ends.
Ends of a cosine theta magnet taking away space from the length of the magnet.
A coil based on the double helix design with ends taking away space from the length of the magnet.
Coil based on the serpentine design showing the loss in the length from one magnet end.
In conventional cosine theta design and in most other conductor dominated designs, the field in a magnet is primarily determined by the turns near the midplane (horizontal axis), while those at other angles are needed for good field quality. Cosine theta magnet design is a two-step process. In first step, the cross-section is designed to modulate the angular distribution of turns for an effective cosine theta function and in the second profile and length of the turns in the end is modulated for good field quality and lower peak field on the conductor.
The conventional conductor-dominated design involves a two-step process. First the coil cross section is optimized for the body of the magnet to create a cosine (nθ) type azimuthal current distribution:
I(θ) = Io COS(nθ)
Then, in the second step, the ends are optimized to minimize the field harmonics to practically create an integrated cosine theta current distribution in the end section with a peak field on the conductor. This 2-step optimization creates a magnet with low integral harmonics but, unfortunately, also one that has a magnetic length that is smaller than the coil length, typically by a coil diameter/(n). For the typical magnet, the main issue is that the field is primarily determined by the turns at the midplane which do not extend over the entire coil length. Also, end spacers are needed to reduce the effective current density in the ends to minimize the integrated field harmonics.
The Optimum Integral Design is a one step process where the length of the midplane turn is made essentially equal to the coil length (end-to-end) with the bend radius of the turns in the ends approaching zero. If there are no spacers in the ends or in the straight section, and if all turns are spaced equally, then the length of successive turns decreases linearly from the midplane to the pole. However, the length and distribution of turns is modulated with the help of a few spacers in the body and the ends so that the current distribution (in the integral sense) becomes proportional to cosine (nθ). The desired integral modulation is obtained with the help of a computer program after distributing a total of “N” turns in a few end blocks and/or in a few cross-section blocks. The size of the spacers between the blocks is optimized to achieve an integral distribution varying azimuthally as:
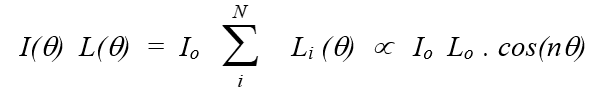
Since the cosine theta modulation is normalized to the current Io times the length Lo (Lo is the end-to-end coil length), this equation suggests that the integral field of the magnet may be closer to a typical 2D field times the mechanical length of the coil (Lo). This is a significant improvement over the designs discussed above where the loss in effective magnetic length from Lo was about a coil diameter/(n).
The optimum integral design opens a new window for building efficient short magnets with a dipole with length shorter than coil diameter, a quadrupole with length shorter than coil radius and sextupole with length shorter than one third of coil diameter, with the example design presented in the paper listed below.
The design is also used in the Phase I and Phase II STTR with the proof-of-principle dipole being built and tested for the Electron Ion Collider.
